Image Processing Project Results

In this project, I implemented methods that:

Part 1: Fun with Filters

For the first part, I applied edge detection using finite difference filters in both the x and y directions (dX and dY). The matrices used are as follows:

        Dx = [1, -1]
        Dy = [[1, 0]
              [0, -1]]

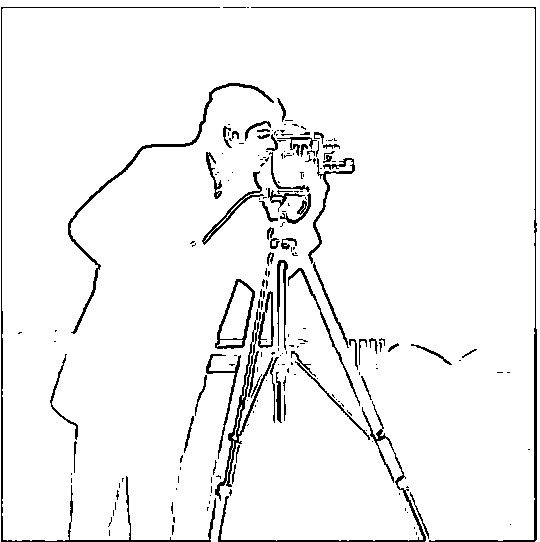
The results are presented in order of dX, dY, gradient magnitude, and binarized gradient magnitude. The cutoff for binarizing the gradient magnitude was 0.3.

First, calculate the partial derivatives in both the x and y directions of the cameraman image by convolving the image with finite difference operators, Dx and Dy. This can be done using convolve2d from the scipy.signal library. Once the partial derivatives are computed, combine them to generate the gradient magnitude image using the following formula:

Gradient Magnitude = sqrt(Dx2 + Dy2)

Part 1.1: Finite Difference Operator Results

Part 1.1 dX Part 1.1 dY Part 1.1 Gradient Magnitude Part 1.1 Binarized Gradient Magnitude

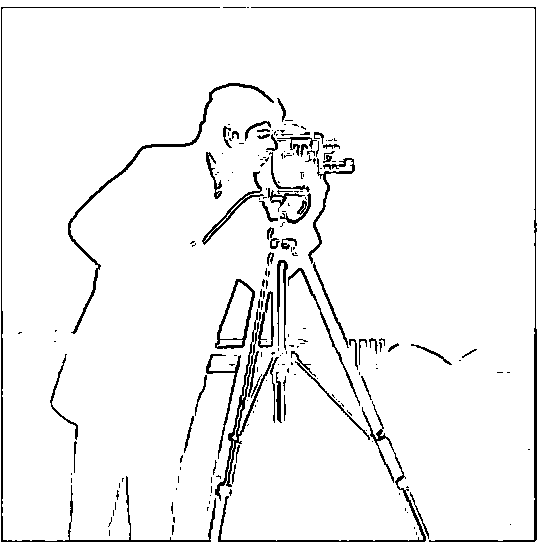
Part 1.2: Derivative of Gaussian (DoG) Filter Results

After applying the Gaussian filter, the outputs were more smoothed out, and the binarized gradient magnitude became thicker due to the spreading effect of the Gaussian filter. The threshold for binarizing the gradient magnitude was 0.3.

Below are the results after applying the Gaussian filter, and it was confirmed that these outputs are the same exact results pixel-wise as when using vanilla Gaussian convolution.

Part 1.2 dX Part 1.2 dY Part 1.2 Gradient Magnitude Part 1.2 Binarized Gradient Magnitude

Here are the vanilla versions of the Gaussian convolution applied to the image. The results are confirmed to be identical pixel-wise to the results shown above:

Part 1.2 Vanilla dX Part 1.2 Vanilla dY Part 1.2 Vanilla Gradient Magnitude Part 1.2 Vanilla Binarized Gradient Magnitude

Part 2: Fun with Frequencies

Part 2.1: Image Sharpening

In this section, I applied image sharpening using the unsharp masking technique. Below is the equation used for sharpening the image:

                f_sharp = f + α(f - f * g) = f * ((1 + α)e - αg)

By adjusting the parameter α, we can control how much sharpening is applied. The results for α = 0 (no sharpening), α = 1, α = 2, and α = 5 are shown below.

Sharpened Image Alpha 0 Sharpened Image Alpha 1 Sharpened Image Alpha 2 Sharpened Image Alpha 5

Sharpening Results for Different Scenes:

Below are additional sharpening results for three different scenes: Singapore vibrant, Paris Versailles, and a fast-paced image. Each row shows the results with α = 0, α = 1, α = 2, and α = 5 for the same scene.

Singapore Vibrant (Alpha 0) Singapore Vibrant (Alpha 1) Singapore Vibrant (Alpha 2) Singapore Vibrant (Alpha 5)
Paris Versailles (Alpha 0) Paris Versailles (Alpha 1) Paris Versailles (Alpha 2) Paris Versailles (Alpha 5)
Fast Paced Image (Alpha 0) Fast Paced Image (Alpha 1) Fast Paced Image (Alpha 2) Fast Paced Image (Alpha 5)

Blurring and Sharpening Paris Versailles Image

The following results demonstrate first applying a Gaussian blur to the Paris Versailles image and then sharpening it. This technique enhances edges and details that were softened by the blur. The images below show the results for different values of α: 0, 3, and 5.

Blurred and Sharpened Paris Versailles Image (Alpha 0) Blurred and Sharpened Paris Versailles Image (Alpha 3) Blurred and Sharpened Paris Versailles Image (Alpha 5)

Part 2.2: Hybrid Images

In this section, I created hybrid images by combining different frequency components of two images:

Derek Hoiem and Nutmeg

Derek Picture Nutmeg Picture Hybrid Image of Derek and Nutmeg

Spidermen: Tom Holland and Andrew Garfield

Below are images of Tom Holland and Andrew Garfield, along with their Fourier transforms and the resulting hybrid images. I particularly enjoyed creating this hybrid, as it turned out to be a favorite among my roommates, who thought it looked really cool. Tom Holland is passed through a high frequency pass filter while Andrew Garfield's rendition of spiderman is passed through a low pass filter instead.

Tom Holland Andrew Garfield Tom Holland Fourier Transform Andrew Garfield Fourier Transform Spiderman Hybrid Image Color Spiderman Hybrid Fourier Image

Additionally, here is the Fourier transform of combining both Spidermen together, represented by the following hybrid image:

Fourier Hybrid Image of Spidermen

Superman and Bruce Wayne

Finally, below are the hybrid failed example results from combining Superman and Bruce Wayne since I am a big DC fan as well (so here is some variety):

Bruce Wayne Superman Superman and Bruce Wayne Hybrid Image

Part 2.3: Multiresolution Blending - Oranges and Apples

Below are images demonstrating Gaussian and normalized Laplacian stacks applied to both oranges and apples very cool blends were created here!:

Gaussian Stack Levels - Oranges

Orange Gaussian Level 0 Orange Gaussian Level 1 Orange Gaussian Level 2 Orange Gaussian Level 3 Orange Gaussian Level 4

Normalized Laplacian Stack Levels - Oranges

Orange Normalized Laplacian Level 0 Orange Normalized Laplacian Level 1 Orange Normalized Laplacian Level 2 Orange Normalized Laplacian Level 3 Orange Normalized Laplacian Level 4

Gaussian Stack Levels - Apples

Apple Gaussian Level 0 Apple Gaussian Level 1 Apple Gaussian Level 2 Apple Gaussian Level 3 Apple Gaussian Level 4

Normalized Laplacian Stack Levels - Apples

Apple Normalized Laplacian Level 0 Apple Normalized Laplacian Level 1 Apple Normalized Laplacian Level 2 Apple Normalized Laplacian Level 3 Apple Normalized Laplacian Level 4

Final Blended Image

Orple Image

Part 2.4: Multiresolution Blending - Image Spline

Finally, the multiresolution blending was applied to different sets of images. Below are the original images alongside their blended results along with different horizontal, vertical, and gradient-based masks. I also tried a segmentation model, but results were less successful:

Northern Lights Ocean Views Ocean Blended Image Sahara Desert Sahara Blended Image Sahara Nonlinear Mask Batman vs Spiderman Blended Image Ocean View Horse on Ocean Blended Image Spider-Man Multiverse

In addition to completing the required tasks, I also took on the Bells and Whistles extra credit by implementing color-based Gaussian/Laplacian stacks and hybrid images as described in the project. I found it really enjoyable to learn these techniques, which I typically associate with video and photo editing!